Let’s Grothendieck Everything In Sight (Week 5)

Last time I talked about how to get some notion of a topological space pointed by an n-dimensional hole. However, this construction wasn’t entirely satisfactory to me because the category was too connected.

Here’s what I mean by that:

Consider the disjoint union $S^1 +S^1$ , the identity function $\mathrm{id}: S^1 + S^1 \to S^1 +S^1$ , and let the the generators of $H_1(S^1+S^1)$ be labeled by $a$ and $b$ . Then, there is a map from $(id, b-a): (S^1+S^1, a) \to (S^1+S^1,b)$ even though they live in different path components. This doesn’t match my intuition about what pointing a space should mean. A pointed space should specify a subset of your topological space which you care about and morphisms between these pointed spaces should preserve that subset. This is not the case for the morphism $(id, b-a)$ because the continuous map $id$ sends the subspace corresponding to $a$ to $a$ instead of $b$ which lives in a different path component.

To fix this problem we will have to do homology the “right”* way; using simplicial sets. This is something I learned recently in John Baez’s class. You can find notes from this class here. Emily Riehl also has a nice introduction to the subject.

Definition: Let $\Delta$ be the category of non-empty finite ordinals and order preserving maps. This is called the simplex category and its objects can be thought of as the following sequence of shapes: dot, line segment, triangle, tetrahedron, etc. These are called simplices.

A simplicial set is a functor $F: \Delta^{op} \to \mathsf{Set}$ . The order preserving functions in $\Delta^{op}$ describe which simplices are faces of each other. So a simplicial set assigns to each basic shape a set of things which have that shape and to each face map a function encoding which of these things are faces of each other. The sum of this data is meant to describe a topological space which is pieced together using simplices. Compositionality is all the rage right now and a nice way to think of simplical sets is as a compositional approach to topology; topological spaces are built from simpler, better understood spaces. Elegantly, morphisms between simplicial sets are natural transformations. The category where objects are simplicial sets and and morphisms are natural transformations is denoted $\mathsf{sSet}$ .

Simplicial sets are functors…but I’d like them to be categories. If only there were some way to turn a functor into a category?

For a simplicial set $F: \Delta^{op} \to \mathsf{Set}$ , it’s Grothendieck construction $\int F$ is a category with the following data:

Objects are tuples $([n], K)$ where $n$ is a finite ordinal and $K$ is an element of $F([n])$ i.e. an n-dimensional simplex
A morphism $f: ([n], K) \to ([m],L)$ is a morphism $f \in \Delta^{op}$ such that $F(f)(K) =L$ . Note that because $F$ is a functor into $\mathsf{Set}$ the morphism components don’t have any contribution from the fibres.

We can think of the Grothendieck construction as a way to pack up a simplicial set into one category where the objects are specific instances of simplices and the morphisms encode specific instances of their boundary. This category is a way to get the actual space that your simplicial set is describing rather than presenting it in pieces.

Given a topological space we can always turn it into a simplical set. Every object $[n] \in \Delta^{op}$ can be realized as a topological space: $[1]$ gives a point called $\Delta_1$ , $[2]$ gives an interval called $\Delta_2$ , $[3]$ gives a triangle called $\Delta_3$ and so on ad infinitum. We can use these geometric realizations to probe a topological space in the following way.

For a topological space $X$ , we can form a simplicial set $S(X) : \Delta^{op} \to \mathsf{Set}$ called the singular simplicial set of $X$ . $S(X)$ sends a non-empty ordinal $[n]$ to the set $\mathrm{Hom}_{\mathsf{Top}} (\Delta_n, X)$ . and morphism $f: [n] \to [m]$ in $\Delta^{op}$ to the function

$S(X)(f) : \mathrm{Hom}_{\mathsf{Top}} (\Delta_n, X) \to \mathrm{Hom}_{\mathsf{Top}} (\Delta_m, X)$

given by pre-composition with $f$ . Normally this map would go in the other direction because it is built using the contravariant hom-functor. However, because we are using $\Delta^{op}$ rather than $\Delta$ we get a map defined covariantly. $S$ extends to a functor

$S: \mathsf{Top} \to \mathsf{sSet}$

which sends a continous map

$f: X \to Y$

to the natural transformation between simplicial sets given by post-composition. For an ordinal $[n]$ we have a map $S(f)_n: \mathrm{Hom}_{\mathsf{Top}} (\Delta_n, X) \to \mathrm{Hom}_{\mathsf{Top}} (\Delta_n, Y)$ which sends a map $a: \Delta_n \to X$ to the composite $f \circ a: \Delta_n \to Y$ . These maps are the components of a natural transformation $S(f): S(X) \to S(Y)$ .

We can compose $S$ with $\int$ to get a functor

$\mathbb{S} = \int \circ S : \mathsf{Top} \to \mathsf{Cat}$

Now let’s integrate this! A meta-Grothendieck construction if you will.

$\int \mathbb{S}$ is a category where

an object is a pair $(X, K)$ where $X$ is a topological space and $K$ an n-dimensional simplex in the singular simplical set of $X$ . Recall that these elements are maps $\Delta_n \to X$ so we can think of $K$ as the realization of some n-dimensional simplex inside of $X$ .
A morphism $(f, d): (X,K) \to (Y,L)$ is a continuous function $f: X \to Y$ and a map $d: \int \circ S (f) (K) \to L$ in $\int \circ S (Y)$ . Let’s unpack this. $f$ induces a map from $\int \circ S(X) \to \int \circ S (Y)$ given by composition and the morphisms in $\int \circ S (Y)$ encode the boundaries and gluings of our simplices. So first we turn the simplex $K$ into a simplex of $Y$ using $f$ and then include it in another simplex or take a boundary to get the simplex $L$ .

Now objects in $\int \mathbb{S}$ have the property I want from pointed objects. If $K$ is a singular simplex of $X$ and $f$ maps $K$ to a simplex $K'$ of $Y$ then $L$ must either be the boundary of $K'$ or vice versa in order to get a map $(X, K)$ to $(Y,L)$ in $\int \mathbb{S}$ . You can think of morphisms in this category as continuous maps which preserve a simplex up to a boundary or inclusion.

Another reason why $\int \mathbb{S}$ is better than last week’s is that includes n-dimensional data for every n whereas the previous category only knew about a fixed dimension n. Simplicial sets (with some extra properties) give models of $(\infty, 1)$ -groupoids called quasi-categories. With this in mind, the category $\int F$ may help you get a notion of pointed $(\infty,1)$ -groupoids – whatever that means – maybe one of you can help me figure that out.

Open ended question: In the category of pointed topological spaces, there is a nice coproduct called the wedge sum, which takes the disjoint union of two topological spaces and identifies their points together. Define a similar construction in $\int F$ which identifies entire n-simplices together. Is this a coproduct?

*Here “right” is defined to mean “using category theory”

6 thoughts on “Let’s Grothendieck Everything In Sight (Week 5)”

Dan Christensen says:

November 4, 2018 at 2:45 pm

The construction of a category from a simplicial set given near the top of the post is called the “category of simplices.” See, for example,

https://ncatlab.org/nlab/show/category+of+simplices

LikeLike

1. jadeedenstarmaster says:
  
  November 6, 2018 at 4:45 am
  
  Thanks! I’m trying to figure out if this answer’s John’s question about being a left adjoint. The nLab article mentions that it preserves colimits so it should have a right adjoint.
  
  LikeLike
  
John Baez says:

November 3, 2018 at 12:30 am

By the way, I was not familiar with your way to turn simplicial sets into categories – it’s nice! But it’s too nice to be new. I’m guessing it’s an adjoint of the more familiar nerve of a category.

LikeLike

1. jadeedenstarmaster says:
  
  November 4, 2018 at 4:18 am
  
  Thanks!
  
  LikeLike
  
John Baez says:

November 3, 2018 at 12:29 am

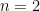There’s a famous way to turn a category into a simplicial set, called its “nerve”. In simple terms, an n-simplex in the nerve of a category C is a chain of composable morphisms $x_0 \to x_1 \to \cdots \to x_n$ . (Draw these for $n = 2$ and you’ll see how to get a category.) More fancily, we notice that the ordinal $[n]$ is a poset and thus a category, and define the set of n-simplices in the nerve of C to be $\mathrm{hom}( [n], C)$ . This clearly extends to a functor from $\Delta^{\mathrm{op}}$ to $\mathrm{Set}$ , i.e. a simplicial set.

Okay, so there’s a “nerve” functor from $\mathrm{Cat}$ to the category of simplicial sets. Your method of turning simplicial sets into categories has just got to be an adjoint of this. Which is it: left or right?

LikeLike

1. jadeedenstarmaster says:
  
  November 4, 2018 at 4:22 am
  
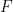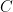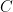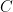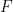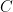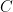  I’m having trouble constructing an adjunction like this because there is a level shift. Let $F$ be a simplicial set, $C$ be a category and $N(C)$ the nerve of $C$ . Then a functor from $\int F$ \to $C$ makes an assignment of the simplices of $F$ to the objects of $C$ . Because the simplices in $N(C)$ are built from the the morphisms of $C$ it’s hard to see how an assignment to the objects of 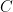$C$ could give a map to these simplices.
  
  LikeLike